Archive for October 2013
Monday, October 14, 2013
Introduction
A major advantage of analyzing circuits using Kirchhoff's laws like we did in Chapter 3 is that we can analyze a circuit without modifying the original configuration but the major disadvantage is that it will take some time to solve it because of the long and complex circuitry.
Linear Property
Linear property is the linear relationship between cause and effect of an element. This property gives linear and nonlinear circuit definition. The property can be applied in various circuit elements. The homogeneity (scaling) property and the additivity property are both the combination of linearity property.
The homogeneity property is that if the input is multiplied by a constant k then the output is also multiplied by the constant k. Input is called excitation and output is called response here. As an example if we consider ohm’s law. Here the law relates the input i to the output v.
Mathematically, v= iR
If we multiply the input current i by a constant k then the output voltage also increases correspondingly by the constant k. The equation stands, kiR = kv
The additivity property is that the response to a sum of inputs is the sum of the responses to each input applied separately.
Using voltage-current relationship of a resistor if
v1 = i1R and v2 = i2R
Applying (i1 + i2) gives
V = (i1 + i2)R = i1R+ i2R = v1 + v2
We can say that a resistor is a linear element. Because of the voltage-current relationship satisfies both the additivity and the homogeneity properties.
We can tell a circuit is linear if the circuit both the additive and the homogeneous. A linear circuit always consists of linear elements, linear independent and dependent sources.
What is linear circuit?
A circuit is linear if the output is linearly related with its input.
The relation between power and voltage is nonlinear. So this theorem cannot be applied in power.
See a circuit in figure 1. The box is linear circuit. We cannot see any independent source inside the linear circuit.

Figure 1
The linear circuit is excited by another outer voltage source vs. Here the voltage source vs acts as input. The circuit ends with a load resistance R. we can take the current I through R as the output.
Suppose vs = 5V and i = 1A. According to linearity property if the voltage is multiplied by 2 then the voltage vs = 10V and then the current also will be multiplied by 2 hence i = 2A.
The power relation is nonlinear. For example, if the current i1 flows through the resistor R, the power p1 = i12R and when current i2 flows through the resistor R then power p2 = i22R.
If the current (i1 + i2) flows through R resistor the power absorbed
P3 = R(i1 + i2)2 = Ri12 + Ri22 + 2Ri1i2 ≠ p1 + p2
So the power relation is nonlinear. Circuit solution method superposition is based on linearity property.
Superposition
The superposition principle states that the voltage across (or current through) an element in a linear circuit is the algebraic sum of the voltages across (or current through) that element due to each independent source acting alone.
To apply this principle for analysis, we must follow these procedures:
1. Turn off all independent sources except one. Find the output (voltage or current) due to that source.
2. Repeat Step 1 for each independent source.
3. Add the contribution of each source to find the total output.
Also:
*Superposition is based on circuit linearity
*Must analyze as many circuits as there are independent sources
*Dependent sources are never turned off
*As with examples, is usually more work than combining resistors, the node voltage analysis, or mesh current analysis
*Is an important idea
*If you want to consider a range of values for an independent source, is sometimes easier than these methods
*Although multiple circuits must be analyzed, each is simpler than the original because all but one of the independent sources is turned off
*Will be necessary when we discuss sinusoidal circuit
Source Transformation is the replacement of a voltage in series with a resistor by a current source in parallel with a resistor or vice versa. the two circuits are equivalent if they have the same current-voltage relationship at their terminals

*A two terminal circuit element is defined by its voltage-current relationship
*Relationship can be found by applying a voltage source to the element and finding the relationship to current
*Equivalently, can apply a current source and find relationship to voltage
*If two elements have the same, they are interchangable

Thevenin's theorem: a linear two-terminal circuit is electrically equivalent to a voltage source in series with a resistor

Norton's theorem: a linear two-terminal circuit is electrically equivalent to a current source in parallel with a resistor
Suppose we have a voltage source or battery whose internal electrical resistance is Ri and a load resistance RL is connected across this battery. Maximum Power Transfer Theorem determines the value of resistance RL for which the maximum power will be transferred from source to it. Actually the maximum power, drawn from the source, depends upon the value of the load resistance. There may be some confusion let us clear it.

Power delivered to the load resistance,

To find the maximum power, differentiate the above expression with respect to resistance RL and equate it to zero. Thus

Thus in this case, the maximum power will be transferred to the load when load resistance is just equal to internal resistance of the battery.
Maximum Power Transfer Theorem can be applicable in complex network as follows
A resistive load in a resistive network will abstract maximum power when the load resistance is equal to the resistance viewed by the load as it looks back to the network. Actually this is nothing but the resistance presented to the output terminals of the network. This is actually Thevenin equivalent resistance as we explained in Thevenin's theorem if we consider the whole network as a voltage source. Similarly if we consider the network as current source, this electrical resistance will be Norton equivalent resistance as we explained in Norton theorem.
Source Transformation
Source Transformation is the replacement of a voltage in series with a resistor by a current source in parallel with a resistor or vice versa. the two circuits are equivalent if they have the same current-voltage relationship at their terminals

*A two terminal circuit element is defined by its voltage-current relationship
*Relationship can be found by applying a voltage source to the element and finding the relationship to current
*Equivalently, can apply a current source and find relationship to voltage
*If two elements have the same, they are interchangable
Thevenin's Theorem

Thevenin's theorem: a linear two-terminal circuit is electrically equivalent to a voltage source in series with a resistor
Norton's Theorem

Norton's theorem: a linear two-terminal circuit is electrically equivalent to a current source in parallel with a resistor
Maximum Power Transfer
Suppose we have a voltage source or battery whose internal electrical resistance is Ri and a load resistance RL is connected across this battery. Maximum Power Transfer Theorem determines the value of resistance RL for which the maximum power will be transferred from source to it. Actually the maximum power, drawn from the source, depends upon the value of the load resistance. There may be some confusion let us clear it.

Power delivered to the load resistance,

To find the maximum power, differentiate the above expression with respect to resistance RL and equate it to zero. Thus

Thus in this case, the maximum power will be transferred to the load when load resistance is just equal to internal resistance of the battery.
Maximum Power Transfer Theorem can be applicable in complex network as follows
A resistive load in a resistive network will abstract maximum power when the load resistance is equal to the resistance viewed by the load as it looks back to the network. Actually this is nothing but the resistance presented to the output terminals of the network. This is actually Thevenin equivalent resistance as we explained in Thevenin's theorem if we consider the whole network as a voltage source. Similarly if we consider the network as current source, this electrical resistance will be Norton equivalent resistance as we explained in Norton theorem.
Introduction
Having understood the fundamental laws of circuit theory (Ohm's Law and Kirchhoff's Law), we are now ready to apply these law to create a new two powerful techniques for circuit analysis: the nodal analysis which is based on a systematic application of Kirchhoff's Current Law (KCL), and mesh analysis which is based on a systematic application of Kirchhoff's Voltage Law (KVL).
NODAL ANALYSIS
Nodal Analysis of electronic circuits is based on
assigning Nodal voltages at various nodes of the
circuit with respect to a reference and then
finding these nodal voltages to analyze the
circuit.
Simple representation of Nodal Voltages shown
in figure:
As shown in Figure, a node is a point
in a circuit where two or more wires
meet. At these nodes one can assign
a nodal voltage with respect to the
reference ground shown.
(Conditions to solve for NODAL)
NODAL ANALYSIS: INDEPENDENT SOURCES ONLY
* First we find the number of KCL equations (These are used to find
the nodal voltages). N -1 = n, here N = number of equations, n =
number of nodes.
* Then we write the KCL equations for the nodes and solve them to
find the respected nodal voltages.
* Once we have these nodal voltages, we can use them to further
analyze the circuit.
* SuperNode: Two Nodes with a independent Voltage source
between them is a Super node and one forms a KVL equation for it.
MESH ANALYSIS
Mesh Analysis involves solving electronic circuits
via finding mesh or loop currents of the circuit.
This is done by forming KVL equations for
respected loops and solving the equations to find
individual mesh currents.
We simply assume clockwise current flow
in All the loops and find them to analyze the circuit. Also any independent current source in a loop. Becomes the loop current as current in series is
Same.
Introduction
We have considered three passive elements
(resistors, capacitors, and inductors) and one
active element (the op-amp) individually, Now
will consider circuits that these contains various
combinations of two or three of the passive
elements. We shall examine two types of simple
circuits: a circuit comprising of a resistor and a capacitor
called RC Circuit and a circuit
compromising of a resistor and a inductor called RL Circuit
Source-Free RC Circuit
A source-free RC circuit occurs when its dc source is suddenly disconnected.
The energy already stored in the capacitor is released to the resistors.
Our objective is to determine the circuit response, which, for pedagogic reasons, we assume to be the voltage v(t) across the Capacitor. we can assume that at time t = 0, the initial voltage is:
v(0) = V0
with the corresponding value of the energy stored
This shows that the voltage response of the RC circuit is an exponential decay of the initial voltage. Since the response is due to the initial energy stored and the physical characteristics of the circuit and not due to some external voltage or current source, it is called the natural response of the circuit.
The natural response of a circuit refers to the behavior (in terms of voltages and currents) of the circuit itself, with no external sources of excitation.
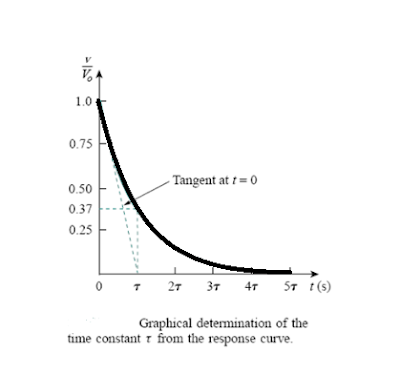
As t increases, the voltage decreases toward zero. The rapidity with which the voltage decreases is expressed in terms of the time constant, denoted by the lower case Greek letter tau, τ.
The smaller the time constant, the more rapidly the voltage decreases, that is, the faster the response.
This is illustrated in A circuit with a small time constant gives a fast response in that it reaches the steady state (or final state) quickly due to quick dissipation of energy stored, whereas a circuit with a large time constant gives a slow response because it takes longer to reach steady state.
At any rate, whether the time constant is small or large, the circuit reaches steady state in five time constants.
THE SOURCE- FREE RL CIRCUIT
Consider the
series connection of a resistor and an inductor, as shown in Figure. Our goal
is to determine the circuit response, which we will assume to be the current i(t) through the inductor. We select the
inductor current as the response in order to take advantage of the idea that
the inductor current cannot change instantaneously. At t = 0, we assume that the inductor has an initial current I0 or
i (0) = Io
with the
corresponding energy stored in the inductor as

Singularity
Functions
Singularity
functions (also called switching functions) are very useful in circuit analysis. Because if we understand singularity
functions, it will help us make sense of the response of first-order circuits
to a sudden application of an independent DC voltage or current source and good
approximations to the switching signals that arise in circuits with switching
operations, it provide a compact description of some circuit phenomena, especially
the step response of RC or RL circuits and functions that are either
discontinuous or have discontinuous derivatives. And the three most widely used
singularity functions in circuit analysis are the unit step, the unit
impulse, and the unit ramp functions.
Introduction
All the methods developed so far for the analysis of linear resistive circuits are applicable to circuits that contain capacitors and inductors.
Unlike the resistor which dissipates energy, ideal capacitors and inductors store energy rather than dissipating it.
Capacitor
A capacitor is formed from two conducting plates separated by a thin
insulating layer.
 If a current i flows, positive change, q, will
If a current i flows, positive change, q, willaccumulate on the upper plate. To preserve
charge neutrality, a balancing negative charge
will be present on the lower plate.
Types of Capacitor
 Capacitor symbol represents the two separated
Capacitor symbol represents the two separatedplates. Capacitor types are distinguished by
the material used as the insulator.
Polystyrene: Two sheets of foil separated by a
thin plastic film and rolled up to save space.
Values: 10 pF to 1 nF.
Ceramic: Alternate layers of metal and ceramic
(a few μm thick). Values: 1 nF to 1 μF.
Electrolytic: Two sheets of aluminium foil
separated by paper soaked in conducting
electrolyte. The insulator is a thin oxide layer
on one of the foils. Values: 1 μF to 10mF.
Electrolytic capacitors are polarised: the foil with the oxide layer must
always be at a positive voltage relative to the other (else explosion).
Negative terminal indicated by a curved plate in symbol.

Inductors
Inductors are formed from coils of wire, often
around a steel or ferrite core.
Types of Inductors
As with many electrical devices, different models exist for
specific applications. Couples multilayer, ceramic core, and molded inductors
are all common types found in commercial and industrial applications:
Coupled Inductors
Coupled inductors exhibit magnetic flux that is dependent on
other to which they are linked. When mutual inductance is needed, coupled
inductors are often used. A transformer is a kind of coupled inductor.
Multi-Layer Inductors
This particular type of inductor consists of a layered coil,
wound multiple times around the core. As a result of the multiple layers and
the insulation between them, multi-layer inductors have a high inductance level.
Ceramic Core Inductors
Although there are numerous kinds of cores, a ceramic core
inductor is unique in having a dielectric ceramic core, meaning it cannot store
a lot of energy but has very low distortion and hysteresis.
Molded Inductors
These inductors are molded using plastic or ceramic
insulation. Often used in circuit boards, they can assume either a cylindrical
or bar formation, with windings featuring terminations at each end.
Formula
Capacitors
Parallel Capacitors
CT = C1 + C2 + C3 + … + Cn
Series Capacitors
CT = 1 / (1/C1 + 1/C2 + 1/C3 ... + 1/Cn)
Inductors
Series Inductance
LT = L1 + L2 + L3 + … + Ln
Parallel Inductance
LT = 1 / (1/L1 + 1/L2 + 1/L3 ... + 1/Ln)
Sunday, October 13, 2013
Introduction
An electric circuit is formed by interconnecting components
having different electric properties. It is therefore important, in the
analysis of electric circuits, to know the properties of the involved
components as well as the way the components are connected to form the circuit.
In this introductory chapter some ideal electric components and simple
connection styles are introduced. Without resort to advanced analysis
techniques, we will attempt to solve simple problems involving circuits that
contain a relatively small number of components connected in some relatively
simple fashions. In particular we will derive a set of useful formulae for
dealing with circuits that involve such simple connections as ``series'',
``parallel'', and ``delta''.
SI base units
an internationally accepted system of physical units, using
the meter, kilogram, second, ampere, kelvin, mole, and candela as the basic
units of length, mass, time, electric current, temperature, amount of
substance, and luminous intensity
SI Prefixes
SI prefixes are used to form decimal multiples and
submultiples of SI units.
They should be used to avoid very large or very small
numeric values.
The prefix attaches directly to the name of a unit, and a
prefix symbol attaches directly to the symbol for a unit.
This is measured in units called coulombs, C,
after Charles Coulomb who made the first precise measurements of the effects of
charges on each other way back in 1785. In chemistry thus far, charge is merely
referred to as 1+ or 2- or +3, it is enough to merely refer to the number of
electrons lost or gained.
A man by the name of Robert Millikan actually made a precise
measurement of the electronic charge value early this century.
It turned out to be extremely small, -1.6x10-19 coulombs.
From what we know of the atom and the number of them in a crystal, we should
not be so surprised.
Current (I ) and charge are linked through
time. Effectively, to measure current we count the passing electrons in one
second and ask ourselves, "how much charge has passed?"
The formula which applies linking these elements is
Current = Amount of charge passing
time in seconds
The unit of current is coulombs per second or ampere (
amp, A).
In symbol terms
I = ΔQ
t
POTENTIAL DIFFERENCE OR VOLTAGE
We have all heard of "voltage" V, more
correctly potential difference, PD. Most small modern batteries are supposed to
be 1.5 or 9 volts. A car battery is slightly over 12 volts. The mains power is
supposed to be 240 volts. So, what is this value, how different is it to
current?
Remember the rafts - they had to be lifted to the top of the
run by a continuously moving ramp or conveyer belt - they were given
gravitational potential energy- which they then lost mostly in the rapid. The
amount of energy would depend on the mass of the raft as well as the height ( Ep =
mgh ). In fact the height alone, all other things being standardised (m,g) is a
measure of the energy lost.
Electrons however, move because of the rules of charges, not
gravity. They move because electrical potential energy is gained or lost. This
is not easy to visualise because of our lack of experience with this energy so
-we will translate them into terms of rafts and rivers.
The electrons are given electrical potential energy by the
battery. They lose a tiny amount in the wiring because no wiring you will come
across is perfect ( perfect wiring does exist - it is called a
"superconductor") but loses the vast bulk of the energy in the player
or lamp or refrigerator to make that device do the work you want - play music
or whatever.
Potential Difference = change in energy between two
points in the circuit
amount of charge involved in measuring energy
PD (V) = ΔEnergy of Q
Q
Power and Energy
What is power?
Power is the rate of using or supplying energy:
Power = Energy Power is measured in watts (W)
Time Time is measured in seconds (s)
Energy is measured in (J)
where:
|
P = power in watts (W)
V = voltage in volts (V)
I = current in amps (A)
|
or:
|
P = power in milliwatts (mW)
V = voltage in volts (V)
I = current in milliamps (mA)
|
What is Energy?And by the way you can use the PIV triangle to help you remember the three versions of the power equations. Use it in the same way as the Ohm's Law triangle. For most electronic circuits the amp is too large, so we often measure current in milliamps (mA) and power in milliwatts (mW). 1mA = 0.001A and 1mW = 0.001W.
The amount of energy used (or supplied) depends on the power
and the time for which it is used:
Energy
= Power x Time
Saturday, October 12, 2013
Introduction
In this chapter we will tackle about some techniques that is commonly applied in circuit design and analysis. These techniques includes combining resistors in series or parallel, voltage division, current division and delta-to-wye and wye-to-delta transformations.
Ohm's Law
To make a current flow through a resistance there must be a voltage across that resistance. Ohm's Law shows the relationship between the voltage (V), current (I) and resistance (R). It can be written in three ways:
V = I × R or I = V or R = V
R I
where:
V = voltage in volts (V)
I = current in amps (A)
R = resistance in ohms (Ω)
or:
V = voltage in volts (V)
I = current in milliamps (mA)
R = resistance in kilohms (kΩ)
For most electronic circuits the amp is too large and the ohm is too small, so we often measure current in milliamps (mA) and resistance in kilohms (kΩ). 1 mA = 0.001 A and 1 kΩ = 1000Ω.
The Ohm's Law equations work if you use V, A and Ω, or if you use V, mA and kΩ. You must not mix these sets of units in the equations so you may need to convert between mA and A or kΩ and Ω.
A node is an uninterrupted segment of wire of any shape. Unless otherwise stated, the wire is considered to be perfect and have no resistance. Therefore, all points on the node have the same voltage. Physically speaking, a node may connect components inches away. However, electrically speaking all the components are connected to a single point. In a schematic representation, node1 extends from the top terminal of the 120V source to the left terminal of the 33 ohm resistor. Node2 includes all the wire segments between R1, R2 and R4. No matter how long the lines extend between components, no potential difference exists between them as long as they are on the same node. A branch is any element connected between two nodes. R4 and R3 are examples of a branch. A loop is any sequence of elements connected between nodes that starts and ends at the same node. You only include a node once in a loop. There may be loops within loops as loop1 and loop2 are within loop3.

Kirchhoff's Law
The voltage across each element and the current through each element in an electric circuit are governed by two general results which are summarized in Kirchhoff's two laws. Since Kirchhoff's laws are derived from general physical properties of electricity, they are applicable to all kinds of electric circuits.
Kirchhoff's Current Law
As a direct consequence of the conservation of charge, namely charge can neither be created nor destroyed, the node, being of negligible physical size, holds no charge. For instance, referring to figure 1.6, the sum of
 ,
,  and
and  must equal zero.
must equal zero. 
Figure 1.6: Kirchhoff's current law
Formally, KCL states that the algebraic sum of the currents in all the branches that converge in a common node is equal to zero. In mathematical form, for n branches converging into a node, KCL states that
 where
where  is the current flowing in the kth branch and its direction is assumed to be pointing towards the node.
is the current flowing in the kth branch and its direction is assumed to be pointing towards the node.Kirchhoff's Voltage Law
When a charged particle is moved from a point to another, the work done is
 , where V is the voltage across the two points and
, where V is the voltage across the two points and  is the amount of charge on the particle. Consider a particular case where the two points are actually the same point in the circuit. In this case, the work done is zero. By the same argument, if a unit charge is moved around a closed path such as the square path shown in figure 1.7, the work done is zero, i.e.,
is the amount of charge on the particle. Consider a particular case where the two points are actually the same point in the circuit. In this case, the work done is zero. By the same argument, if a unit charge is moved around a closed path such as the square path shown in figure 1.7, the work done is zero, i.e.,Figure 1.7: Kirchhoff's voltage law
Formally, KVL states that the algebraic sum of the voltages between successive nodes in a closed path in a circuit is equal to zero. In mathematical form, for a closed path with successive nodes
 , KVL states that
, KVL states thatRemarks -- Any circuit that has a solution must satisfy Kirchhoff's laws. From the properties of independent sources, we can immediately conclude that a circuit cannot be solved if there exists a loop that is formed exclusively of independent voltage sources. Thus, short-circuiting an independent voltage source, as remarked earlier, is a particular case where KVL is violated. Similarly, a circuit cannot be solved if there exists a node to which only independent current sources are connected. Also, open-circuiting an independent current source is a particular case where KCL is violated.
The Voltage Divider
For a single resistor with a voltage across it, Ohm's Law is quite an impressive tool. Put a few resistors together in series, however, and things get even more interesting! The total resistance of resistors in series is simply the sum of their individual resistances. By combining this concept with Ohm's Law we can design one of the most commonly used circuits in a guitar amplifier: the voltage divider.
Problem
Consider the power supply of a Mesa Boogie Bass 400 amplifier. It uses two 150k resistors in series to equalize the voltage across the filter capacitors and to act as bleed resistors that slowly discharge the capacitors when the amplifier is turned off. (If only all amplifiers were designed this way - it would be a much safer world!) The total voltage across both resistors is 534 volts. What is the voltage across each individual resistor?

Solution
The total resistance across both resistors is
150k + 150k = 300k
According to Ohm's Law, the current passing through the resistors is
534/300k = 1.78mA
Thus 1.78mA passes through each of the resistors individually. By applying Ohm's Law once more, we get the voltage across one resistor:
(1.78mA)(150k) = 267V
The Voltage Divider
A voltage divider is often used to attenuate a signal by a prescribed amount. We often see them in guitar amplifier input circuits, for example, where they attenuate the signal to give the guitar player a low-gain input jack. They are also used in the second stage of a paraphase inverter to equalize the amplitudes of the two output phases. Other guitar circuits may not appear to be voltage dividers at first, but we frequently discover that at certain frequencies the components effectively create one. The voltage divider thus represents an essential tool of guitar amplifier design.
Problem
Consider the second stage paraphase inverter of the Gibson GA-20T amplifier. An input signal is applied across 220k and 4.7k resistors in series. The output voltage is the voltage across the 4.7k resistor. Given that the input signal is 1 volt, what is the output voltage?

Solution
The total resistance of both resistors in series is 224.7k. This means that according to Ohm's Law the current is
1/224.7k = 0.00445mA
This current passes through the 4.7k resistor, so according to Ohm's Law, the voltage across it is
(0.00445mA)(4.7k) = 0.021
So the input is 1 volt and the output is 0.021 volts. The output is thus only 2.1 percent of the input. This is quite a bit of attenuation and not a random value picked by the engineers in Kalamazoo. The resistor values were chosen to reduce the input voltage by exactly this amount.
Notice that we computed the output voltage in two separate steps. First we computed the current that passes through both resistors. Then we used this current to determine the output voltage. We really weren't interested in the current. We just needed it as an intermediate step. Let's avoid the middleman and combine the two steps into one equation to simplify the calculation. Looking at our procedures in reverse, the output voltage is
(0.0445mA)(4.7k) = 0.21
and the current is
1/224.7k = 0.0445mA
We combine these into a single equation by noting that the 0.0445mA in the first formula is equal to 1/224.7k in the second. Thus
(1/224.7k)(4.7k) = 0.021
So the output voltage is equal to the input voltage divided by the total resistance in series, times the resistance across the output. This works for any combination of two resistors R1 and R2, as shown in this circuit:

The output voltage is equal to the input voltage times the output resistor R2 divided by the total resistance R1+R2. This is the fundamental Principle of a voltage divider.
Current Division

Consider the circuit shown in figure where two resistors are connected parallel. Supplying voltage for current resistor. From Ohm’s law we get
v = i1R1
= i2R2
or i1 = V/R1, i2 = V/R2
Applying KCL,
i = i1 + i2
Substituting and adding the value in equation (i) then we get,
i = V/R1+ V/R2
= V (1/R1 + 1/R2)
= V/Req
Here Req is the equivalent resistance.
1/Req = (1/R1) + (1/R2)
Or 1/Req = (R1 + R2)/ R1 R2
Req = R1 R2/ (R1 + R2)
Using current divider rule,
I1= R2i/ (R1 + R2)
I2= R1i/ (R1 + R2)
Wye-Delta Transformations
Most of the time we can solve the circuit using our idea of series and parallel connection and ohm’s law or KCL or KVL. But sometimes we encounter some circuit where the formations of elements are neither in series nor in parallel. For example look at the figure of bridge network below:

Now look at the following two formations which look like Wye and Delta. These formations usually found in three phase connections, filters, or in matching networks.

(a) Y netwrk (b) Delta Network

(a) Delta Network

(b) Pie Network
When we analyze a circuit we may find a certain formation to be helpful. And we might want to change one formation into other. Suppose it might helpful for us to work with Wye formation in three phase rather in Delta formation. So we have to know how to transform a Delta network into Wye network.
Delta to Wye conversion:
Look at the figure below:

Now for Delta to Wye conversion:
R1 = (Rb . Rc) / (Ra + Rb + Rc)
R2 = (Rc . Ra) / (Ra + Rb + Rc)
R3 = (Ra . Rb) / (Ra + Rb + Rc)
We don’t have to memorize these formulas rather we can easily remember these.Each resistor of the Wye network is the product of the two adjacent resistors of Delta network, divided by the sum of all three resistors of the Delta network.
Wye to Delta Conversion:
Look at the figure again:

Now for Wye to Delta conversion:
Ra = (R1.R2 + R2.R3 + R3.R1) / R1
Rb = (R1.R2 + R2.R3 + R3.R1) / R2
Rc = (R1.R2 + R2.R3 + R3.R1) / R3
We don’t have to memorize this also. The easy way to remember is, each resistor in the Delta Network is the sum of all possible product formation of Wye network’s resistors taken two at a time, divided by the opposite Wye resistor.
























 is the voltage between nodes j and k.
is the voltage between nodes j and k.